Filogenias¶
La filogenia es el estudio de las relaciones evolutivas. Un análisis filogenético no sólo nos indica las relaciones evolutivas entre las secuencias o especies, cuales descienden de ancestros comunes, también puede indicarnos cuales son las distancias entre ellas. Los métodos de reconstrucción filogenética más habituales asumen que todas las secuencias o especies provienen de partir un ancestro común mediante bifurcaciones.
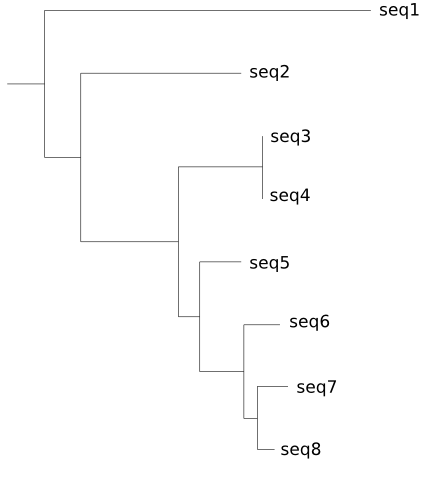
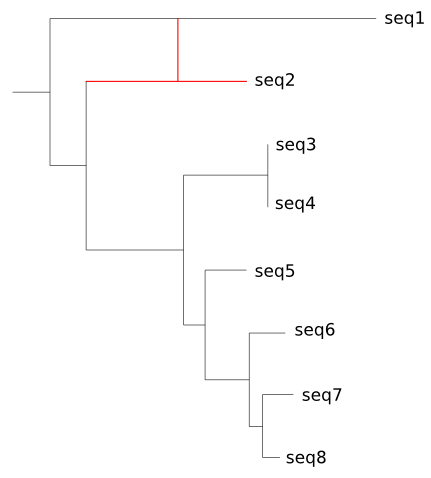
Asímismo asumen que todas las secuencias o especies de las que tenemos información son especies actuales y que ninguna de ellas es un antepasado de cualquiera de las otras.
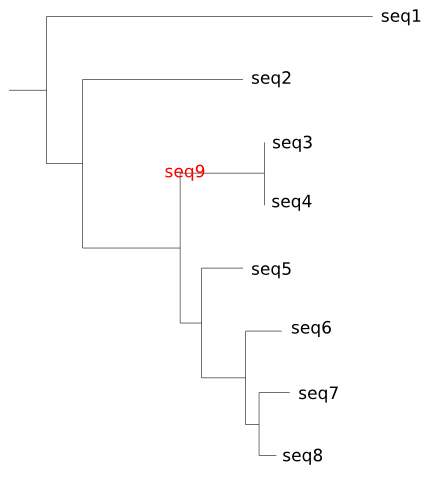
Si estas condiciones no se cumpliesen no sería correcto intentar reconstruir una filogenia mediante los métodos que vamos a comentar. Por ejemplo, si estamos comparando poblaciones pertenecientes a una especie no tiene por que cumplirse que las distintas poblaciones se hayan originado por una simple bifurcación de las anteriores. Es común que varias poblaciones se mezclen por migración y esto no se tiene en cuenta en los métodos de reconstrucción filogenética.
Los métodos filogenéticos nos permiten reconstruir su el árbol que representa la historia evolutiva de las especies a partir de las evidencias experimentales de las que dispongamos. Algunos tipos de evidencias que pueden ser utilizados son:
Datos morfológicos
Genotipos
Secuencias de ADN o de proteínas.
Algunas de las metodologías utilizadas por la filogenética, cómo por ejemplo los árboles UPGMA, son también utilizadas comúnmente en otros ámbitos como, por ejemplo, en el de la taxonomía. En estos casos no se está reconstruyendo una historia evolutiva sino únicamente las relaciones de similitud entre los distintos grupos o individuos clasificados.
Estrictamente hablando las especies no tienen porqué tener una única filogenia. Distintos genes pueden haber tenido una historia distinta. En este caso se podría calcular la filogenia de cada gen o una filogenia consenso de la especie.
Introducción a la filogenia¶
Los métodos filogenéticos reconstruyen árboles (dendrogramas) en los que las ramas y los nodos unen diferentes taxones. Estos taxones pueden ser especies, individuos, genes, etc. Al recorrer las ramas desde los nodos terminales hacia nodo original recorremos la historia evolutiva de ese gen o organismo.
En filogénia se suele utilizar una serie de términos específicos.
Un dendograma es un árbol que representa las relaciones entre los distintos nodos.
Un Clado es una rama del árbol. Representa un conjunto de especies emparentadas por un antepasado común.
Un taxón es un clado al que le ha asignado una categoría taxonómica.
Un filograma es un dendograma en el que la longitud de las ramas se corresponde con el número de cambios o con las distancia entre los nodos.
| -------------- A
| |--|
| | --------- B
| |
| -------------------------C
En un árbol ultramétrico todas las ramas desde el antepasado común hasta el actual tienen el mismo tamaño.
| --------- A
| ------|
| | --------- B
| |
| ----------------C
La raíz es la base de todas las ramas. Los árboles pueden clasificarse en árboles con y sin raíz.
| --------- A
| ------|
| | --------- B
| --|
| |
| ----------------C
|
| --------- A
| ------|
| | --------- B
| |
| |
| ----------------C
Monofilético el el grupo que sólo incluye ramas que provienen de un único antecesor común. Un grupo polifilético incluye ramas que provienen de varios antepasados, por ejemplo, el de los gusanos sería un grupo polifilético. Por último un grupo se denomina parafilético si todos sus miembros provienen de un antepasado común, pero no incluye todos los descendientes del mismo, los reptiles son un ejemplo de grupo parafilético puesto que no incluye a las aves.
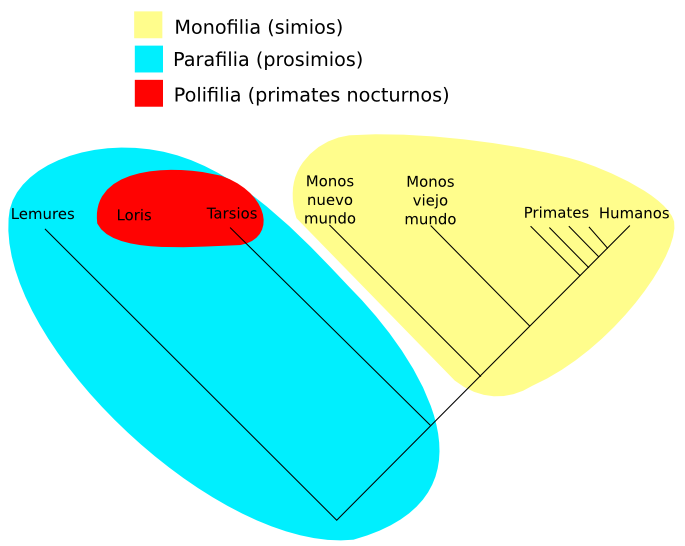
Una politomía es un nodo sin resolver del que parten varias ramas.
| --------------- A
| |
| |-------------- B
| |
| ----------------C
Topología¶
Un dendograma puede ser representado gráficamente de distintos modos equivalentes. Hemos de ser cautos a la hora de decidir qué dendogramas son distintos y cuales no lo son.
| --------- A
| ------|
| | --------- B
| |
| | --------C
| --------|
| --------D
|
| --------- B
| ------|
| | --------- A
| |
| | --------C
| --------|
| --------D
|
| --------- B
| ------|
| | --------- A
| |
| | --------D
| --------|
| --------C
filogenias basadas en secuencias¶
Las filogenias pueden construirse con datos de muchos tipos, pero en este curso nos centraremos en las creadas a partir de secuencias de ADN o proteína. Al utilizar un método de reconstrucción filogenética estaremos asumiendo una serie de premisas:
Cada secuencia es correcta y pertenece a su organismo.
Las secuencias son homólogas y se han originado a partir de un ancestro común.
Cada posición de una secuencia del alineamiento es homóloga a la del resto de secuencias.
Las secuencias evolucionan con un patrón al azar.
Las posiciones del alineamiento evolucionan independientemente unas de otras.
No existe intercambio de información genética entre los diferentes organismos (recombinación).
Además, al hacer el árbol asumimos que las secuencias utilizadas incluyen información suficiente como para resolver el problema. Esta es una asunción que podemos y debemos comprobar por algún método estadístico.
Por último, hay que tener en cuenta que si pretendemos reconstruir un árbol de especies y estamos utilizando una o varias secuencias para hacerlo hemos de asumir que las secuencias elegidas son representativas de las especies incluidas en el análisis. Si no fuese así estaríamos generando un árbol correcto de secuencias, pero no de especies.
Conviene recordar cuales son los distintos tipos de homologías:
Ortólogo: Secuencias homólogas de dos especies diferentes y que provienen de una secuencia común.
Parálogo: Secuencias homólogas de un mismo organismo. Provenientes de duplicaciones génicas.
Xenólogo: Secuencias homólogas de dos especies diferentes pero provienen de una transferencia horizontal.
Alineamientos de secuencias como base de los árboles filogenéticos¶
Los árboles filogenéticos se pueden construir a partir de alineamientos múltiples de secuencias. Ya hemos mencionado que en este caso estamos asumiendo que cada posición en el alineamiento es homóloga. Por lo tanto, construir un buen alineamiento es esencial para la resolución del árbol.
La edición manual de los alineamientos es habitual para conseguir el mejor posible. Como vimos la mayoría de los programas de alineamiento nos dan una solución subóptima (la mejor posible utilizando pocos recursos del sistema), por lo tanto resulta conveniente revisar los alineamientos antes de realizar los árboles.
En general los problemas suelen acumularse en las regiones más variables en las que hay muchas sustituciones o muchos gaps. En estos casos podríamos estar incluyendo posiciones que no son homólogas con lo que estaríamos introduciendo una información espúrea en el análisis. Esta revisión de los alineamiento podemos realizarla con programas desarrollados para tal fin. El Gbloks selecciona bloques según su nivel de conservación y elimina aquellas regiones con gaps o no conservadas para obtener bloques altamente conservados. El trimAI elimina regiones no conservadas y espúreas teniendo en cuenta diferentes parámetros como el número de secuencias con gaps en una posición, regiones con nivel bajo de similitud, etc.
Métodos de construcción de árboles¶
Existen muchos métodos de construcción de árboles. Pueden ser clasificados en distintas familias según se basen en:
distancias.
parsimonia.
máxima verosimilitud.
bayesianos.
Cálculo de distancias¶
La distancia es una medida del grado de divergencia entre dos secuencias. Utilizamos la distancia como una aproximación al tiempo desde que las dos secuencias se separaron. En este caso lo primero que se hace es generar una matriz de distancias por parejas de secuencias a partir del alineamiento múltiple. En estos métodos toda la información de similitudes y diferencias entre dos secuencias queda resumida por un simple número.
Existen diferentes estadísticos para calcular la distancia entre dos secuencias. En teoría podríamos utilizar un estadístico tan sencillo como el porcentaje de posiciones cambiadas entre dos secuencias, pero la mayoría de los estadísticos tienen en cuenta que las posiciones pueden estar saturadas, es decir en el alineamiento vemos los cambios definitivos pero no aquellos que han afectado a la misma posición varias veces. Nuestro objetivo es tener una media de distancia que se comporte linealmente con el tiempo. Debido al problema saturación llegará un momento que aunque aumente el tiempo desde que dos secuencias se separaron las mutaciones quedarán enmascaradas por actuar sobre la misma posición y será difícil contabilizarlas para la distancia. Para solucionar este problema se suele utilizar un modelo de mutación mediante el que intentamos evaluar la distancia real en base a las mutaciones que podemos observar.
Modelos de sustitución¶
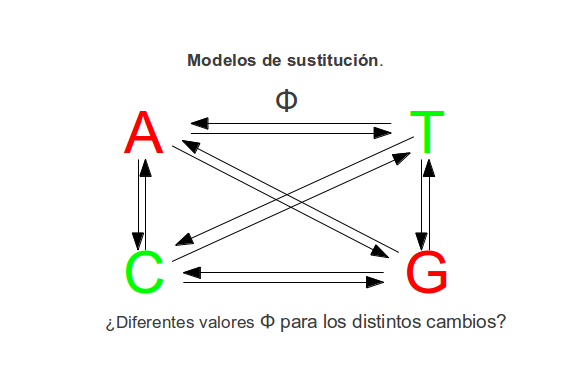
Podemos calcular las distancias entre las secuencias asumiendo distintos modelos de mutación. Hay modelos más sencillos y otros más complejos. Los más sencillos suelen ser modelos demasiado simplificados que no se corresponden demasiado bien con la realidad. Los más complejos tienen el inconveniente de repartir la información filogenética existente en el alineamiento entre demasiados parámetros por lo estos suelen estar peor determinados y sus varianzas suelen aumentar. Según los datos de los que dispongamos el modelo de mutación óptimo puede ser uno u otro. Existen programas, como jModelTest, que pueden probar todos estos modelos en nuestros datos y nos pueden recomendar qué modelo debemos utilizar para realizar un árbol de forma óptima.
A continuación describimos algunos de los modelos de mutación.
Modelo Jukes-Cantor¶
Todas las posiciones evolucionan independientemente. Todas las bases están a igual frecuencia. Todos los cambios se producen a la misma frecuencia. Las mutaciones son fenómenos raros.
d = -3/4 ln (1-4/3p)
p proporción de cambios entre las dos secuencias
Modelo Kimura2-parametros¶
Distingue entre transiciones (purina a purina o pirimidina a pirimidina) y transversiones (purina a pirimidina y viceversa) y asume que frecuencia de los diferentes nucleótidos es igual.
d = -1/2 ln(1-2p-q) - 1/4 ln(1-2q)
p proporción de transiciones y q proporción de transversiones.
Modelo general¶
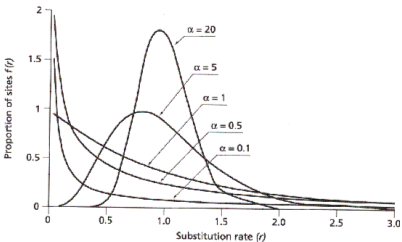
Este es uno de los modelos mas complejos. La frecuencia de los distintos nucleótidos es distinta y la tasa de cambios entre los nucleótidos es diferente para cada tipo. Además a este modelo se le puede añadir que no todas las regiones de la secuencia evolucionan a la misma velocidad (las tasas de sustitución pueden variar a lo largo de la secuencia (Distribución gamma).
Árboles basados en distancias¶
A partir de una matriz de distancia podemos utilizar distintos métodos estadísticos para reconstruir un árbol. Existen numerosos métodos, pero los más utilizados son el UPGMA y el Neighbor-joining. Estos métodos de creación de árboles no son específicos de la filogenia por lo que los veremos comúnmente utilizados para resolver otros tipos de problemas en los que se pretende obtener una clasificación jerárquica.
Estos métodos basados en matrices de distancias son muy rápidos y permiten utilizar secuencias muy largas en un gran número de individuos con unos recursos computacionales de memoria y tiempo muy limitados.
Una vez hemos creado el árbol podemos estudiar cómo de preciso es el ajuste del mismo a la matriz de datos original realizando un test de correlación cofenético. En este test a partir del árbol se calcula una nueva matriz de distancias y esta matriz se compara con la original para estudiar como de bien se correlacionan. También podemos realizar un análisis de bootstrap para validar el árbol.
UPGMA¶
UPGMA es un método de clustering (clasificación) que se basa en la identificación de las parejas más similares y en el cálculo de la media de las distancias entre ellas y el resto de las secuencias para reconstruir el árbol. Resulta conveniente usarlo solo si se cumple la hipótesis del reloj molecular (todas las secuencias han evolucionado a la misma velocidad) dado que genera árboles ultramétricos.
Neighbor-joining¶
El método de neighbor-joining es un método muy utilizado en las filogenias de secuencias. La principal diferencia respecto al UPGMA es que los árboles que genera no son ultraméticos, es por lo tanto el más recomendable si no estamos seguros de que se cumple la hipótesis del reloj molecular, es decir si esperamos que distintas ramas puedan haber evolucionado a distinta velocidad.
Máxima parsimonia¶
El método de máxima parsimonia se basa en la filosofía de que la explicación más simple, la que requiere menos cambios debe ser la correcta. Mediante este método se obtienen árboles que ordenan las ramas de modo tal que se minimiza el número de mutaciones que deben haber ocurrido.
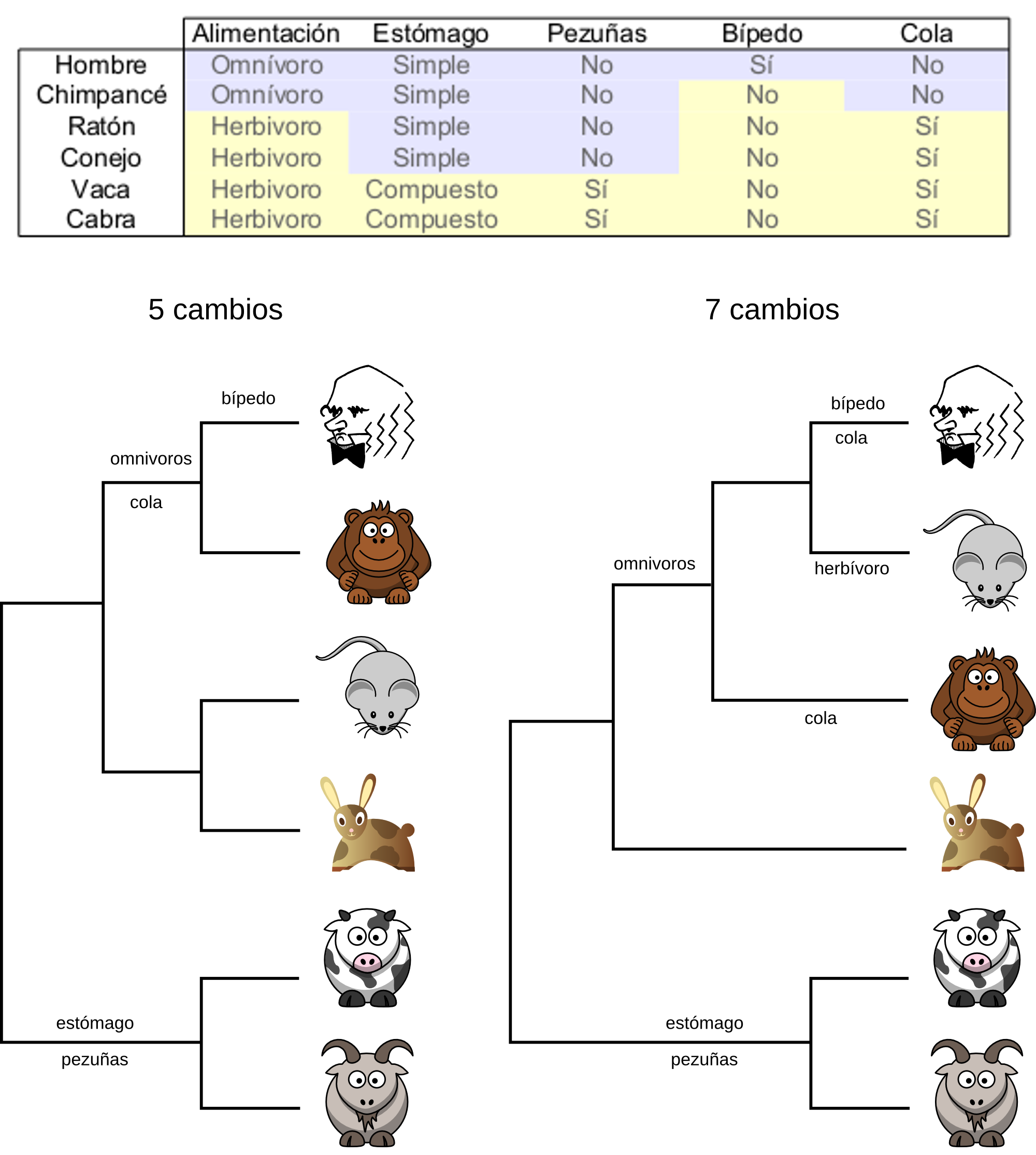
Para elegir el mejor árbol, el árbol que implicase menos cambios, en teoría habría que evaluar todos los árboles posibles. Este evaluación podría hacerse si el número de taxa es pequeño, pero a medida que este número aumenta el número de árbol crece desmesuradamente y no es factible evaluar todos los árboles posibles. En la práctica los programas utilizan un método heurístico para evaluar sólo los árboles más razonables y desechar directamente los más improbables.
El resultado final de un algoritmo de máxima parsimonia no tiene porque ser un único árbol puesto que puede que existan varios árboles que impliquen un mismo número de mutaciones.
Los caracteres pueden ser clasificados en informativos y no informativos.
A aat tcg ctt cta gga atc tgc cta atc ctg
B ... ..a ..g ... .t. ... ... t.. ... ..a
C ... ..a ..c ... ... ..t ... ... ... t.a
D ... ..a ..a ... ..g ..t ... t.t ..t t..
1 2 3 4 5
La posición 1 no es informativa porque no es variable.
La posición 2 sí varía, pero tampoco es informativa puesto que en cualquier árbol que podamos imaginar siempre contribuirá con una mutación. Este tipo de caracteres se denominan autoapomorfías.
La posición 3 es demasiado variable puesto que cambia en todos los individuos. En cualquier árbol siempre contribuirá con un mismo número de mutaciones, 3.
Las posiciones 4 y 5 sí son informativas puesto que indican que dos de los individuos son más cercanos. Estas posiciones no serían explicadas con el mismo número de mutaciones en todos los árboles y por lo tanto pueden utilizarse para discriminar entre ellos. Este tipo de caracteres representan caracteres homólogos derivados (sinapomorfías).
El método de parsimonia ha sido tradicionalmente el preferido por bastantes investigadores, pero presenta algunos problemas estadísticos sistemáticos. Se ha demostrado que éste método, en algunos casos, no garantiza encontrar el árbol correcto incluso teniendo información de un gran número de caracteres informativos. Uno de los casos en los que éste método falla sistemáticamente es el caso en el que algunas ramas sean mucho más largas que otras.
| ----A
| -----|
| | ----------------------------B
| |
| | --------------------------C
| -----|
| ----D
|
Máxima verosimilitud¶
El método de máxima verosimilitud busca el árbol máximoverosímil, es decir, el árbol que es más probable que haya generado los datos que hemos observado. En este método partimos de los datos y de un modelo de evolución. Partiendo de esta base se calcula la probabilidad de que nuestros datos hayan sido generado por los distintos árboles posibles y se devuelve el árbol que presenta una máxima probabilidad.
Para poder calcular uno de estos árboles es imprescindible elegir un modelo de mutación a priori. Una vez determinado el modelo, el algoritmo hará una estima maximoverosímil de los parámetros relativos a las tasas de mutación así como del árbol.
De modo análogo al método de parsimonia en este caso para calcular el árbol más verosímil también deberían explorarse todos los árboles posibles, pero dado que eso es computacionalmente imposible de llevar a cabo también se utilizan métodos heurísticos para explorar tan sólo los árboles más razonables.
Este método tiene la ventaja frente a los de máxima verosimilitud y de parsimonia de utilizar con mayor eficiencia la información filogenética contenida en el alineamiento múltiple. Es decir, dado un mismo alineamiento éste método tiende a generar un resultado más cercano a la realidad. Este método, por ejemplo, no presenta el problema sistemático con las ramas de distinto tamaño que describimos en el método de máxima parsimonia.
La desventaja principal del método es el coste de computación que conlleva. Hasta que los ordenadores no tuvieron una potencia suficiente este método no pudo aplicarse e incluso en los ordenadores modernos puede ser costoso si el número de taxa o la longitud del alineamiento son grandes.
Métodos Bayesianos¶
La inferencia bayesiana calcula una probabilidad posterior para cada árbol posible dado un modelo de evolución y unas observaciones. Es decir, dadas unas observaciones la inferencia bayesiana actualiza las probabilidades de que los árboles sean correctos.
En caso de la filogenia bayesiana dados los datos que hemos observado, normalmente una serie de secuencias, y unas probabilidades a priori se generan unas probabilidades tanto para el conjunto de posibles árboles como para los parámetros del modelo de mutación. En este caso el modelo de mutación también debe ser elegido antes de comenzar la reconstrucción filogenética.
En este método también debería calcularse la probabilidad a posteriori de todos los árboles, pero esto no es computacionalmente posible. La alternativa utilizada consiste en recurrir a cadenas de Markov que permiten ir explorando los árboles más verosímiles. Las cadenas de Markov tienen el inconveniente de caer en mínimos locales por lo que se suelen utilizar con el algoritmo Metropolis-coupled Montecarlo vía Cadenas de Marvok (MCMCMC).
La implementación de referencia en este tipo de reconstrucción filogenética es el software MrBayes.
Este método es el que más tiempo y recursos computacionales requiere, pero suele considerarse como el método que arroja unos mejores resultados.
Árboles con raíz¶
Los métodos que hemos visto producen árboles sin raíz. Un modo de asignar la raíz comúnmente utilizado es incluir un taxa que sabemos a priori que está más alejado filogenéticamente del resto. Por ejemplo, una secuencia de plantas cuando estamos analizando una filogenia de todo el reino animal. Un problema es que en algunos casos si escogemos una secuencia demasiado distinta se puede distorsionar el resto del árbol. Otro modo, menos común, de situar la raíz es asumir que se cumple la hipótesis del reloj molecular de modo que podamos elegir la secuencia más distinta como la más antigua.
Métodos de validación de árboles¶
Un árbol no tiene demasiada utilidad si no evaluamos su significación estadística. Un método filogenético siempre generará un resultado a partir de cualquier conjunto de datos, pero esto no implica que este resultado sea fiable. De algún modo debemos decidir en qué nodos del dendograma podemos confiar y en cuales no.
En los métodos bayesianos los nodos tienen asociados una probabilidad posterior que indica la confianza que podemos tener en ellos, pero en el resto de metodologías debemos utilizar algún método para hacer esta evaluación. Un método ideal consistiría en obtener varios conjuntos de datos independientes y generar a partir de ellos distintos árboles. Comparando qué nodos son compartidos por estos árboles y cuales no podríamos hacernos una idea de qué resulta fiable y qué no. Desgraciadamente este método no resulta práctico en muchas ocasiones por lo que se han desarrollado otros algoritmos que nos ofrecen algo similar a tener varios conjuntos de datos para obtener distintos árboles. Uno de los más utilizados es el bootstrap.
Este método se puede aplicar a todos los métodos y consiste en crear réplicas de los alineamientos a partir del original, eliminando cierto número de posiciones al azar en cada replica. El número final de posiciones se mantiene constante, añadiendo duplicaciones de los sitios que han permanecido. Para cada una de estas réplicas aplicaremos el método de reconstrucción filogenética y generaremos un árbol. El paso final será evaluar para cada nodo el porcentaje de árboles en los que aparece. Los nodos con un alto valor de bootstrap tienen, si se cumplen las asunciones del método utilizado, una probabilidad alta de ser correctos mientras que los que tienen un bajo valor de bootstrap podrían haberse generado simplemente por azar.
Se ha discutido mucho cuales son los valores límite que indicarían que un nodo es fiable y no se ha llegado a conclusiones demasiado claras. Evidentemente un nodo que aparece en el 95 % de los árboles tiene una apariencia de ser sólido mientras que uno que aparezca en un 50% de los árboles no parece demasiado fiable. Pero en los casos intermedios es difícil llegar a una conclusión demasiado clara. Resulta común encontrar dendogramas en los que la discusión se centra en los nodos con valores de bootstrap mayores de 70.
Si generamos el árbol consenso con el programa consense del paquete phylip hay que tener en cuenta que las distancias del árbol obtenido no se corresponden con las distancias basadas en la matriz de distancias o en el número de mutaciones sino con el valor de bootstrap. En este caso particular lo único que nos debe importar es la topología. Para obtener el árbol correcto debemos aplicar los valores de bootstrap obtenidos mediante el remuestreo al árbol obtenido con todos la matriz de datos completa, sin hacer bootstrap.
Programas de filogenias¶
Existen numerosos programas para realizar filogenias: Phylip, MEGA, MrBayes, Phylemon, etc.
Nos vamos a centrar en el MEGA. Es en realidad un paquete de programas que nos permite realizar alineamientos, análisis y árboles filogenéticos mediante diferentes métodos a partir de alineamientos de ADN o proteínas.
