ALINANEAMIENTOS MULTIPLES¶
Definición y diferencias frente a los alineamientos de 2 secuencias¶
Hablamos de alineamientos multiples (MSA) cuando tratamos con mas de dos secuencias. Este tipo de alineamientos requiere un abordaje más complejo que el de pares de secuencias ya que el uso directo de los estadísticos de alineamiento global y local requiere una gran capacidad de cálculo y solo es aplicable a problemas con muy pocas secuencias.
El principal problema que nos plantean los alineamientos múltiples es la posición de los gaps en el alineamiento. En el alineamiento, todas las secuencias tienen que tener la misma longitud y eso se consigue introduciendo gaps.

Algoritmos de construcción progresiva¶
Los programas más utilizados se basan en este tipo de estrategias. No nos garantizan que el alineamiento obtenido sea el mejor posible, pero son capaces de encontrar una solución óptima de forma muy eficaz. Ejemplos de programas basados en estos métodos heurísticos: ClustalW y T-coffe.
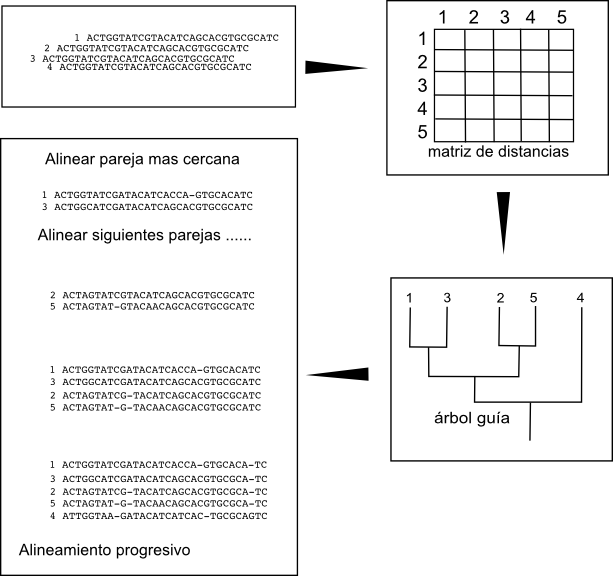
El método consiste en primero realizar alineamientos de dos en dos. A partir de estos alineamientos se construye una matriz de distancias entre las secuencias y un árbol guía basado en estas distancias. Mediante este árbol podemos encontrar las parejas de secuencias más similares.
Al alineamiento del par de secuencias más similar se va añadiendo el resto de secuencias o alineamientos por el orden determinado por el árbol guía.
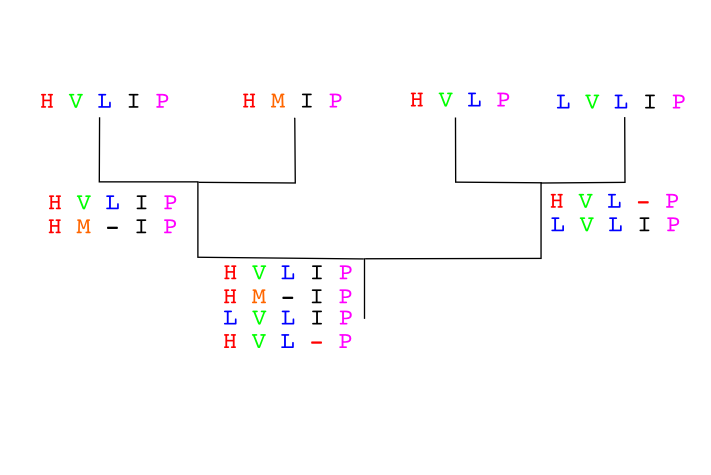
En nuestro ejemplo anterior :
DISTANCIAS:
IMPRESIONABLE X IMPRESO 7/13
IMPRESIONABLE X INCUESTIONABLE 10/14
INCUESTIONABLE X IMPRESO 4/14
El primer alineamiento seria: Incuestionableximpresionable.
IMPRES-IONABLE
INCUESTIANABLE
Posteriormente uniría Impreso
IMPRES-IONABLE
INCUESTIONABLE
IMPRES--O-----
Los programas derivados del clustal (ClustalW y ClustalX (versión gráfica)) incorporan un sistema de puntuación del alineamiento. La puntuación esta basada en la distancia genética entre cada secuencia y la raíz del árbol, teniendo en cuenta la puntuación por los cambios de aminoácidos o nucleótidos. Además de esta puntuación, los gaps y la extensión de los gaps están penalizados. La puntuación del alineamiento global será la suma de la puntuación de los alineamientos de parejas de secuencias. El ClustalW tiende a situar los gaps entre las zonas altamente conservadas en vez de separar estas regiones.

Fig. Alineamiento de tres secuencias altamente conservadas
Fig. Alineamiento con gaps
Problemas de los alineamientos de construcción progresiva¶
Los mayores problemas de este tipo de alineamientos derivan del alineamiento de la primera pareja. Si las dos primeras secuencias son cercanas (muy similares) el alineamiento base probablemente contenga pocos errores. En cambio, si estas dos secuencias son muy divergentes el alineamiento obtenido no será muy adecuado y los gaps y errores se propagarán al resto de secuencias añadidas puesto que este primer alineamiento ya no es modificado al unirse el resto de alineamientos. Para paliar este problema es mejor alinear secuencias del mismo tamaño es decir incluir únicamente en el alineamiento aquellas regiones presentes en todas las secuencias ya que el programa intentara alinear toda la longitud de la secuencia introduciendo gaps en el resto.
Este tipo de alineamientos funciona correctamente para secuencias con cierto grado de conservación y que varíen de forma más o menos continua. Pero a pesar de estos inconvenientes, este tipo de algoritmos suelen encontrar una buena solución con pocos recursos, permitiendo el análisis de muchas secuencias.
Utilidades de los alineamientos múltiples¶
Los alineamientos múltiples son una herramienta fundamental. Estos alineamientos son imprescindibles para realizar estudios posteriores, como por ejemplo:
estudios evolutivos,
análisis de dominios conservados,
estructuras secundarias,
reconocimiento de regiones conservadas en promotores, etc.
Edición de alineamientos multiples.¶
Los alineamientos múltiples generados por estos programas son ficheros de texto que en principio podríamos editar con cualquier editor. Pero algunos formatos no resultan cómodos para ser manejados por un editor de texto o el número de secuencias o su longitud complican la edición.
Existen programas especializados para editar alineamientos, uno de los mas completos es el Bioedit , el cual nos permite además enlazar con diferentes aplicaciones como Blast, primer3, etc. Es un editor gráfico que funciona en windows y, además, es bastante intuitivo en su uso.
